도둑이 보석가게에 배낭을 메고 침입했다.
배낭의 최대 용량은 W이며, 이를 초과해서 보석을 담으면 배낭이 찢어질 것이다.
각 보석들의 무게와 가격은 알고 있다.
배낭이 찢어지지 않는 선에서 가격 합이 최대가 되도록 보석을 담는 방법은?
위의 문제는 대표적인 배낭 채우기 문제이다.
찾아보니 배낭 채우기 문제는 두 가지 유형으로 나뉜다고 한다.
물건(보석)을 자를 수 있을 때의 "Fractional Knapsack"과
자를 수 없을 때의 "0-1 Knapsack Problem"로 나뉜다고 한다.
자를 수 있는 경우는 보통 그리디 알고리즘으로 해결한다고 한다.
이 글에서 다루는, 그리고 보통 많이 다루는 배낭 채우기 알고리즘은 자를 수 없는 경우이다.
배낭 채우기 문제를 푸는 방법은 여러 가지가 있다.
모든 경우의 수를 따지는 브루트 포스와 가장 좋은 것을 우선 선택하는 그리디 알고리즘으로 풀 수도 있지만
가장 효과적인 방법 다이나믹 프로그래밍(DP)으로 푸는 방법이다.
백준 12865번 : 평범한 배낭
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
|
#include <iostream>
#include <algorithm>
using namespace std;
int n, k;
int DP[101][100001];
int w[101];
int v[101];
int main() {
cin >> n >> k;
for (int i = 1; i <= n;i++) {
cin >> w[i] >> v[i];
}
for (int i = 1; i <= n;i++) {
for (int j = 1; j <= k;j++) {
DP[i][j] = DP[i - 1][j];
if (j - w[i] >= 0)
DP[i][j] = max(DP[i][j], v[i] + DP[i - 1][j-w[i]]);
}
}
cout << DP[n][k];
}
|
cs |
다이나믹 프로그래밍은 Memoization(반복되는 계산을 줄이기 위해 메모리에 계산 값을 미리 저장)이 중요하기 때문에 항상 메모리(배열 등)에 어떤 값을 저장할 것인지와 미리 메모리에 값을 저장할 수 있게 하는 점화식이 중요하다.
배열 DP[i][j]는 가방의 무게가 j 일 때 i 번째 물건까지 확인했을 때의 가질 수 있는 최대 가치를 저장한다.
점화식은 i번째 물건(보석)을 배낭에 담을 지에 따라 2가지로 나뉜다.
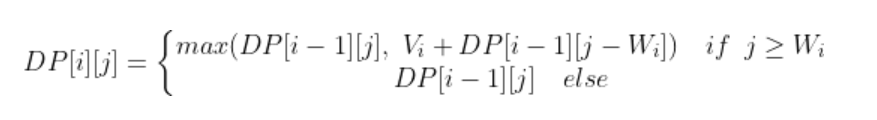
무게를 넘지 않을 때 (i번째 보석을 담는 경우) 값을 비교해서 최댓값으로 최신화하고
무게를 넘을 때 (i번째 보석을 담지 않는 경우) 전 단계의 값을 그대로 가져온다.
이해를 위한 DP배열의 값을 다음과 같다. (문제 참고)
| D P | 보 석 ( i ) | |||||
| 배 낭 무 게 ( j ) |
0 | 1 | 2 | 3 | 4 | |
| 0 | 0 | 0 | 0 | 0 | 0 | |
| 1 | 0 | 0 | 0 | 0 | 0 | |
| 2 | 0 | 0 | 0 | 0 | 0 | |
| 3 | 0 | 0 | 0 | 6 | 6 | |
| 4 | 0 | 0 | 8 | 8 | 8 | |
| 5 | 0 | 0 | 8 | 8 | 12 | |
| 6 | 0 | 13 | 13 | 13 | 13 | |
| 7 | 0 | 13 | 13 | 14 | 14 | |
앞서 설명한 내용과 같이 배열 DP는 최대 가치를 저장한다.
이해를 위해서 DP[3][7]을 한번 살펴보겠다.
DP[3][7]은 허용가능한 무게가 7일 때 3번째 보석까지 확인 했을 때의 최대 가치이다.
2번째 보석(i = 2)까지 확인했을 때에는 1번과 2번 보석을 같이 담을 수 없고, 1번의 보석이 가치(13)가 더 높으므로
배열 DP에선 13을 저장하고 있다.
하지만 i = 3이 되면서 2번째 보석과 3번째 보석을 담을 수 있다. (W[2] + W[3] = 7)
점화식에 따라 계산했을 때 1번 보석의 가치(13)를 담고 있는 DP[2][7] 와
2번 보석과 3번 보석의 가치를 합한 값 ( V[3] + DP[2][4] )을 비교한다.
2번 보석과 3번 보석의 가치를 합한 값(14)가 더 크므로 최신화를 해준다.
이 '0-1 Knapsack' 알고리즘에서 중요한 것은 점화식을 이해하는 것이다.
최대값을 비교할 때 오는 DP[i-1][j-W[i]] 는 이전 보석의 가치를 의미한다.
이 점만 잘 이해하면 된다. ^^7
'개인 공부 > 알고리즘' 카테고리의 다른 글
| [알고리즘] 재귀 & 그리디 알고리즘 (0) | 2023.05.03 |
|---|---|
| [알고리즘] 정렬 & 탐색 알고리즘 (0) | 2023.04.28 |
| [알고리즘] 에라토스테네스의 체 (0) | 2022.07.01 |
| [알고리즘] 유클리드 알고리즘(최대공약수, 최소공배수 구하기) (2) | 2021.07.03 |
| [알고리즘] 가장 긴 증가하는 부분수열(LIS) (0) | 2021.06.23 |


댓글