728x90
💻 알고리즘
📌 플로이드-워샬 알고리즘이란?
그래프 이론 중 하나로 다익스트라 알고리즘과 비슷하게 노드와 노드 사이의 최단거리를 구하는 알고리즘이다.
이 알고리즘의 특징과 동작 원리는 다음과 같다.
✔️ 특징
- 모든 노드 간의 최단거리를 구한다. 따라서 2차원의 공간이 필요하다.
- 음의 비용을 가지는 그래프에서도 사용할 수 있다.
- O(n^3)의 시간복잡도를 가진다. (3중 반복문)
- 다이나믹 프로그래밍의 성질을 가진다.
✔️ 동작 원리
- 거쳐 가는 노드를 기준으로 알고리즘이 수행한다.
- a → b의 비용과 a → k → b의 비용을 비교해서 더 작은 비용으로 최신화한다.
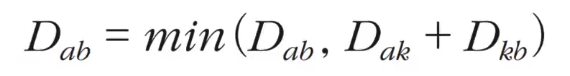
INF = int(1e9)
# 정점과 간선 개수 입력
vertex, edge = map(int, input().split())
# 그래프 초기화
graph = [[INF] * (vertex+1) for _ in range(vertex+1)]
for i in range(1, vertex+1):
graph[i][i] = 0
# 간선 입력받기
for _ in range(edge):
start, end, cost = map(int, input().split())
graph[start][end] = cost
# 플로이드-워셜 알고리즘
for k in range(1, vertex+1):
for a in range(1, vertex+1):
for b in range(1, vertex+1):
graph[a][b] = min(graph[a][b], graph[a][k] + graph[k][b])
# 알고리즘이 적용된 그래프 출력
for x in range(1, vertex+1):
for y in range(1, vertex+1):
if graph[x][y] == INF: print(0, end=' ')
else: print(graph[x][y], end=' ')
print()
'개인 공부 > TIL' 카테고리의 다른 글
| TIL : git 사용하기 (10) (0) | 2022.08.24 |
|---|---|
| TIL : Kruskal(크루스칼) 알고리즘 (9) (0) | 2022.08.21 |
| TIL : Two-Pointer 알고리즘 (7) (0) | 2022.08.08 |
| TIL : Union-Find 알고리즘, Disjoint Set 자료구조 (6) (0) | 2022.08.07 |
| TIL : 다익스트라 알고리즘 (5) (0) | 2022.08.01 |

댓글